
The inspiration for this project came from a question in a popular calculus textbook at the end of a section on related rates. Here is an altered version of that quesiton:
The minute hand on a clock is 0.8m long, while its hour hand is 0.55m long. How fast is the distnace between the endpoints of the clock hands changing at some time?
In this module, I will use python to animate a clock that constantly updates this rate of change; and I will write a code that takes the time in from a user (in HH:MM format) and outputs the rate of change at that time.

We let $L$ be the length of the minute hand that is $\theta_m$ radians clockwise from the positive y-axis; $l$ is the length of the hour hand that is $\theta_h$ radians clockwise from the positive y-axis; $R$ is the distance between the endpoints of the two hands. The goal is to determine the rate at which $R$ is changing with respect to time. We begin by noting the positions at which the endpoints of both hands lie in our coordinate system.
$$
\text{End of Minute Hand}\equiv(x_m, y_m)= (L\sin\theta_m,L\cos\theta_m)
$$
$$
\text{End of Hour Hand}\equiv(x_h, y_h)= (l\sin\theta_h,l\cos\theta_h)
$$
Via the distance formula we know that
$$
R = \sqrt{(x_h - x_m)^2 + (y_h - y_m)^2}
$$
\begin{equation}
R=\sqrt{(l\cos\theta_h - L\cos\theta_m)^2 + (l\sin\theta_h - L\sin\theta_m)^2}
\end{equation}
Now our job is as simple as taking the derivative with respect to time $t$ of both sides of equation (1), and doing some algebra -- note that the derivative calls for some semi-extensive usage of the chain rule.
\begin{multline*}
\frac{dR}{dt} = \frac{1}{2R}\Biggl[2(l\cos\theta_h - L\cos\theta_m)\left(-l\frac{d\theta_h}{dt}\sin\theta_h + L\frac{d\theta_m}{dt} \sin\theta_m \right) \\
+ 2(l\sin\theta_h - L\sin\theta_m)\left(l\cos\frac{d\theta_h}{dt}\cos\theta_h - L\frac{d\theta_m}{dt}\cos\theta_m\right)\Biggl]
\end{multline*}
From here, we see that the 2 in our denimator cancels out with the 2s from within the square brackets; and now we will expand this by multiplying these binomials together.
\begin{multline*}
\frac{dR}{dt} =\frac{1}{R}\Biggl[
\Biggl(-l^2\frac{d\theta_h}{dt}\cos\theta_h\sin\theta_h + lL\frac{d\theta_m}{dt}\cos\theta_h\sin\theta_m + lL\frac{d\theta_h}{dt}\cos\theta_m\sin\theta_h \\
\qquad\qquad\qquad\qquad-L^2\frac{d\theta_m}{dt}\cos\theta_m\sin\theta_m\Biggl) \\
+ \Biggl(l^2\frac{d\theta_h}{dt}\cos\theta_h\sin\theta_h - lL\frac{d\theta_m}{dt}\sin\theta_h\cos\theta_m - lL\frac{d\theta_h}{dt}\sin\theta_m\cos\theta_h \\
+L^2\frac{d\theta_m}{dt}\cos\theta_m\sin\theta_m\Biggl)
\Biggl]
\end{multline*}
The first and final terms of both polynomials cancel out with one another, leaving us with
\begin{equation*}
\frac{dR}{dt} = \frac{lL}{R}\left[\frac{d\theta_m}{dt}(\sin\theta_m\cos\theta_h-\sin\theta_h\cos\theta_m) + \frac{d\theta_h}{dt}(\sin\theta_h\cos\theta_m-\sin\theta_m\cos\theta_h)\right]
\end{equation*}
We will now simplify this further by two means. First, we take note that the angular speeds of each clock hand is constant -- hence, we will make the following substitutions:
$$
\frac{d\theta_m}{dt} = \omega_m \qquad\qquad\qquad \frac{d\theta_h}{dt} = \omega_h
$$
Finally we will take advantage of the following difference of angles identity to get our final expression:
$$
\sin\alpha\cos\beta - \sin\beta\cos\alpha = \sin(\alpha-\beta)
$$
\begin{equation}
\frac{dR}{dt} =\frac{lL}{R}\left[\omega_m\sin(\theta_m-\theta_h) + \omega_h\sin(\theta_h-\theta_m)\right]
\end{equation}
Examining equation (2), we see that the rate at which the distance between the endpoints of the clock hands depends on the angular speed of the hands -- which makes sense -- and the angular positions of the hands. Thinking about the arguments of our sine functions shows that we have a value of zero when the hands are parallel or anti-parallel.
Note that at this point I realized you can rewrite equation (2) as follows (since sine is an odd function). {The first code block below uses equation (2), although using equation (3) would be more elegant.}
\begin{equation}
\frac{dR}{dt} = \frac{lL}{R}(\omega_m - \omega_h)\sin(\theta_m-\theta_h)
\end{equation}
Let us now find an extremum of this function by taking the derivative again and setting the result equal to zero, rembembering that $R$ is indeed dependent on time.
$$
\frac{d^2R}{dt^2} = \frac{lL}{R}(\omega_m-\omega_h)^2\cos(\theta_m-\theta_h) - \frac{l^2L^2}{R^2}(\omega_m-\omega_h)^2\sin^2(\theta_m-\theta_h) = 0
$$
$$
\Rightarrow \frac{d^2R}{dt^2} = \cos(\theta_m-\theta_h) - \frac{lL}{R}\sin^2(\theta_m-\theta_h) = 0
$$
\begin{equation}
\tan(\theta_m - \theta_h)\sin(\theta_m-\theta_h) = \frac{R}{lL}
\end{equation}
From here we can expand our expression for $R$ out and make use of the difference of angles formula for cosine (in hindsight, if one does this from the start, it makes this problem much less tedious) to rewrite equation (4) as follows
$$
\frac{d^2R}{dt^2} = \tan^2(\theta_m - \theta_h)\sin^2(\theta_m-\theta_h) - \frac{l^2 + L^2 + 2lL\cos(\theta_m-\theta_h)}{lL} = 0
$$
I know of no way to analytically solve such a beast. We can however make a plot of the second derivate of $R$ w.r.t. time as a function of the angle between the minute hand and the hour hand ($\theta_m-\theta_h)$ and see where it crosses the x-axis. Here is that plot:
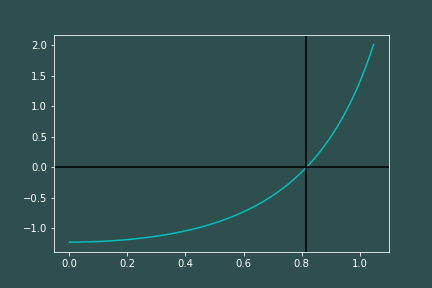
This curve crosses the x-axis at around 0.8145rad, which is roughly 46.7 degrees. This means that the extremums of the rate of change of the distance between the endpoints of the clock hands (both the max and the min) occur when the minute hand and hour hand are seperated by about 47 degrees -- this can be verified visually in the animation below.
Now lets animate this guy. Below, find the code used to make both the labeled plot from above (commented out) as well as the code to produce the animation that you will find below the block of code.
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.animation as animation
# create a function for the distance between the clock hands
def R_distance(x_m, y_m, x_h, y_h):
R = np.sqrt((x_h-x_m)**2 + (y_h-y_m)**2)
return R
# create a function to find dR/dt (RoC=RateOfChange)
def R_RoC(theta_h, theta_m):
R = R_distance(L*np.sin(theta_m), L*np.cos(theta_m), l*np.sin(theta_h), l*np.cos(theta_h))
Rdot = (l*L/R)*(omega_m*np.sin(theta_m-theta_h) + omega_h*np.sin(theta_h-theta_m))
return R, Rdot
# first let's build a picture of a clock
with plt.rc_context({'axes.edgecolor':'white', 'xtick.color':'white', \
'ytick.color':'white', 'figure.facecolor':'darkslategrey',\
'axes.facecolor':'darkslategrey','axes.labelcolor':'white',\
'axes.titlecolor':'white'}):
# square figure
fig = plt.figure(figsize=(6,6))
# subplot for animation
ax = plt.subplot(1,1,1, aspect='equal')
# get rid of axis ticks
ax.tick_params(axis='both', colors="darkslategrey")
# plot will go from (-1.25,-1.25) to (1.25,1.25) clock will be of r=1
ax.set_xlim(-1.25, 1.25)
ax.set_ylim(-1.25,1.25)
# setup domain and range for border of clock (circle of radius=1)
radius = 1
circ_domain = np.linspace(-1,1,250)
circ_range_top = [np.sqrt(radius - x**2) for x in circ_domain]
circ_range_bot = [-np.sqrt(radius - x**2) for x in circ_domain]
# plot top of clock
ax.plot(circ_domain,circ_range_top, color="black", lw=2)
# plot bottom of clock
ax.plot(circ_domain,circ_range_bot, color="black", lw=2)
# fill in background of clock
ax.fill_between(circ_domain,circ_range_top,circ_range_bot,color="lavender")
# create numbers to put on clock
number_list = range(1,13,1)
num_list = [str(num) for num in number_list]
# locations of numbers
num_radius = 0.87*radius
num_x = []
num_y = []
num_angs = []
for i in range(1,13,1):
ang = np.pi*i/6
num_angs.append(ang)
num_x.append(num_radius*np.sin(ang))
num_y.append(num_radius*np.cos(ang))
# put the numbers on the clock
for x, y, num in zip(num_x, num_y, num_list):
ax.text(x, y, num, color="black", fontsize=15, ha='center', va='center', fontfamily='monospace')
# length of hands
L = 0.8*radius # length of minute hand
l = 0.55*radius # length of hour hand
# the following chunk of code creates the unanimated-labeled clock
# =============================================================================
# # minute hand
# ax.plot([0,L*np.sin(np.pi/6)],[0,L*np.cos(np.pi/6)], color='k', lw=3,zorder=100)
# # hour hand
# ax.plot([0,l*np.sin(3*np.pi/6)],[0,l*np.cos(3*np.pi/6)], color='k', lw=6,zorder=100)
# # distance between their points
# ax.plot([L*np.sin(np.pi/6),l*np.sin(3*np.pi/6)],[L*np.cos(np.pi/6),l*np.cos(3*np.pi/6)], color='magenta', ls='--',zorder=10)
# # vertical line
# ax.plot([0,0], [0,radius], color='blue', ls='--')
# # angle curves
# domain_minute = [x for x in np.linspace(0,.24*np.sin(np.pi/6),80)]
# range_minute = [np.sqrt(0.24**2-x**2) for x in domain_minute]
# domain_hour = [x for x in np.linspace(0,.18*np.sin(3*np.pi/6),80)]
# range_hour = [np.sqrt(0.18**2-x**2) for x in domain_hour]
# ax.plot(domain_minute,range_minute, color='k', lw=1.3)
# ax.plot(domain_hour,range_hour, color='k', lw=1.3)
# # labels
# ax.text(0.15, 0.47, r'$L$', fontsize=15, color='k')
# ax.text(0.25, -0.14, r'$l$', fontsize=15, color='k')
# ax.text(0.01, 0.31, r'$\theta_m$', fontsize=15)
# ax.text(0.14, 0.11, r'$\theta_h$', fontsize=15)
# ax.text(0.51,0.33, r'$R$', fontsize=15)
# =============================================================================
# angular speeds of hands
omega_m = 2*np.pi/3600
omega_h = omega_m/12
# create lists of angles for animation and calculations
# we want 24 hours, each frame is 1s; 1440 frames
rotations = 2 # how many full rotations of hour hand we want
n = int(60*12*rotations*2.15) # number of frames (increased from 1440)
theta_h_values = np.linspace(0,2*np.pi*rotations,n)
theta_m_values = np.linspace(0,2*np.pi*12*rotations,n)
# find the R and Rdot values at each point
R_values = []
Rdot_values = []
i = 0
while i < len(theta_h_values):
R, Rdot = R_RoC(theta_h_values[i], theta_m_values[i])
R_values.append(R)
Rdot_values.append(Rdot)
i += 1
# make our animation
ims = []
index = 0
while index < len(theta_h_values):
# animate the minute hand
min_hand, = ax.plot([0,L*np.sin(theta_m_values[index])],[0,L*np.cos(theta_m_values[index])], color='k', lw=3, zorder=100)
# animate the hour hand
hour_hand, = ax.plot([0,l*np.sin(theta_h_values[index])],[0,l*np.cos(theta_h_values[index])], color='k', lw=6, zorder=100)
# line connecting ends of the hands
R_line, = ax.plot([L*np.sin(theta_m_values[index]),l*np.sin(theta_h_values[index])],\
[L*np.cos(theta_m_values[index]),l*np.cos(theta_h_values[index])], color="purple", ls='--', zorder=10)
# text for R value in top left and Rdot value in the top right
R_val = ax.text(-1.15, 1.08, "R ="+str(round(R_values[index],4))+"m", fontsize=15, color='white')
Rdot_val = ax.text(-1.15, -1.15, r"$\frac{dR}{dt} =$"+str(round(Rdot_values[index]*1000,5))+"mm/s", fontsize=15, color='white')
# append ims list for each iteration
ims.append([min_hand,hour_hand, R_line, R_val, Rdot_val])
# iterate index by however many frames we want to move forward
index += 1
ani = animation.ArtistAnimation(fig, ims, interval=1000)
writervideo = animation.FFMpegWriter(fps=34)
ani.save('../images/clockHandsNew0.mp4', writer=writervideo)
Now we will write a code that takes the time in from a user (in HH:MM format) and outputs the rate of change at that time.
import numpy as np
import matplotlib.pyplot as plt
# create a function for the distance between the clock hands
def R_distance(x_m, y_m, x_h, y_h):
R = np.sqrt((x_h-x_m)**2 + (y_h-y_m)**2)
return R
def R_RoC(theta_h, theta_m):
R = R_distance(L*np.sin(theta_m), L*np.cos(theta_m), l*np.sin(theta_h), l*np.cos(theta_h))
Rdot = (l*L/R)*(omega_m-omega_h)*np.sin(theta_m-theta_h)
return Rdot
def time_to_angles(times):
hour = times[0]%12 # mod 12 to account for pm ('military' time)
minute = times[1]
theta_h = np.pi*(hour/6 + minute/360)
theta_m = np.pi*minute/30
return theta_m, theta_h
while True:
time = input("What time is it (HH:MM)? ").split(":")
time = [int(t) for t in time]
if not (1 <= time[0] <= 24) or not (0 <= time[1] <= 59):
print("Invalid time. Hours are between 1 and 24; minutes are between 0 and 59.")
else:
break
# angular speeds of hands
omega_m = 2*np.pi/3600
omega_h = omega_m/12
# lengths of hands
L = 0.8
l = 0.55
theta_m, theta_h = time_to_angles(time)
Rdot = R_RoC(theta_h, theta_m)
print(f'dR/dt = {Rdot*1000:.5f} mm/s'.format())
Here are some example inputs/outputs from this code: