∮ 4th-Order Runge-Kutta vs. Euler-Cromer

I have already compared the results of using the 4-order Runge-Kutta method and the Euler-Cromer method on my page about the elastic double pendulum. Here, we will take a look at how the results from using these two methods differ for the simple pendulum, damped pendulum, and driven pendulum.

∯ Simple Pendulum

The equations of motion for a simple pendulum may be written as follows $$ \dot{\theta} = \omega $$ $$ \dot{\omega} = -\frac{g}{l}\sin\theta $$ where $g$ is acceleration due to gravity, $\theta$ is the angle our pendulum makes with the vertical, $\omega$ is the angular speed of the pendulum. Here, I let $l=1.05$m, and dropped our pendulum from rest letting the initial angular displacement be $\theta_i = \pi/2$ radians. Our coordinate system is set up such that the pendulum starts with zero energy (KE is zero because it is dropped from rest, and graviational potential energy is 0 because we let the pivot point of our pendulum be at $y=0$m). Here is what the time evolution of this system looks like:

I made the animation using the Euler-Cromer method, with a time step of $dt = 0.01$s. Let us take a look at the energy vs time graph:

E vs. t Euler-Cromer ($dt = 0.01$)

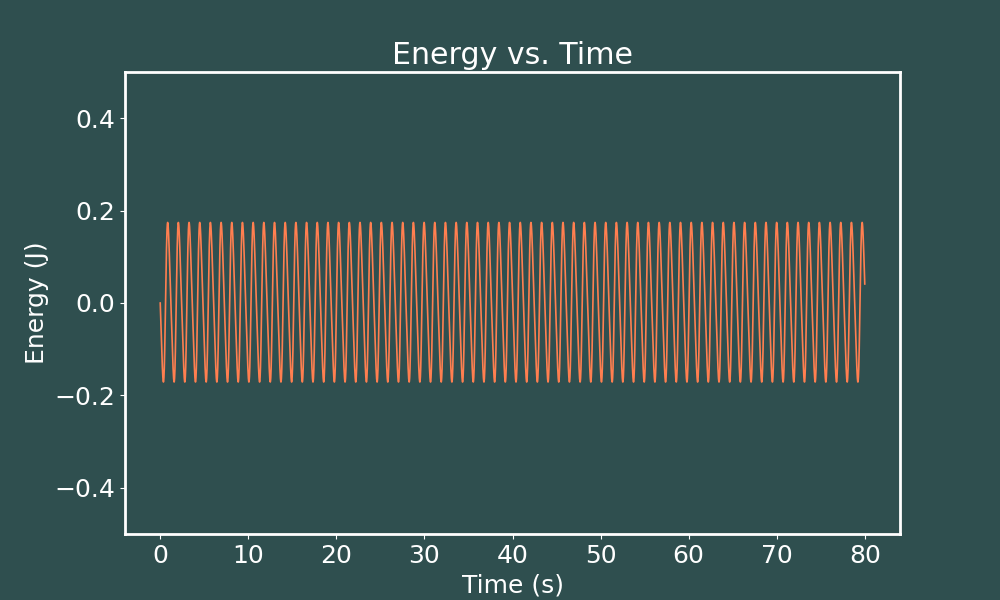
We see that our energy does indeed start at zero, but is not constant. It oscillates such that roughly $-0.2\text{J}\leq E \leq 0.2$J, but $E_{max}$ and $E_{min}$ do not appear to change. Let use not make our time step smaller and see what happens.

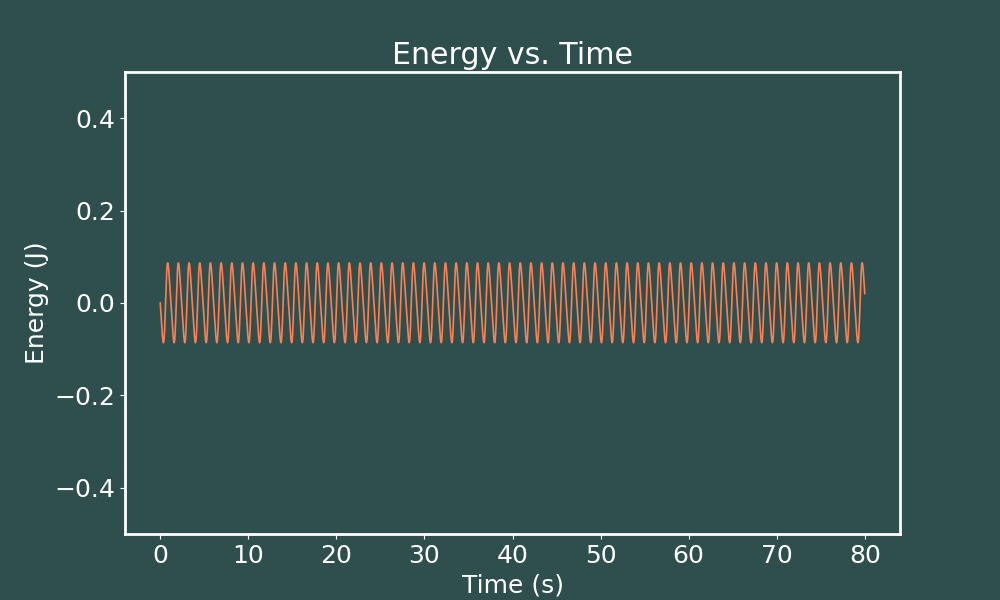
E vs. t Euler-Cromer ($dt = 0.005$)

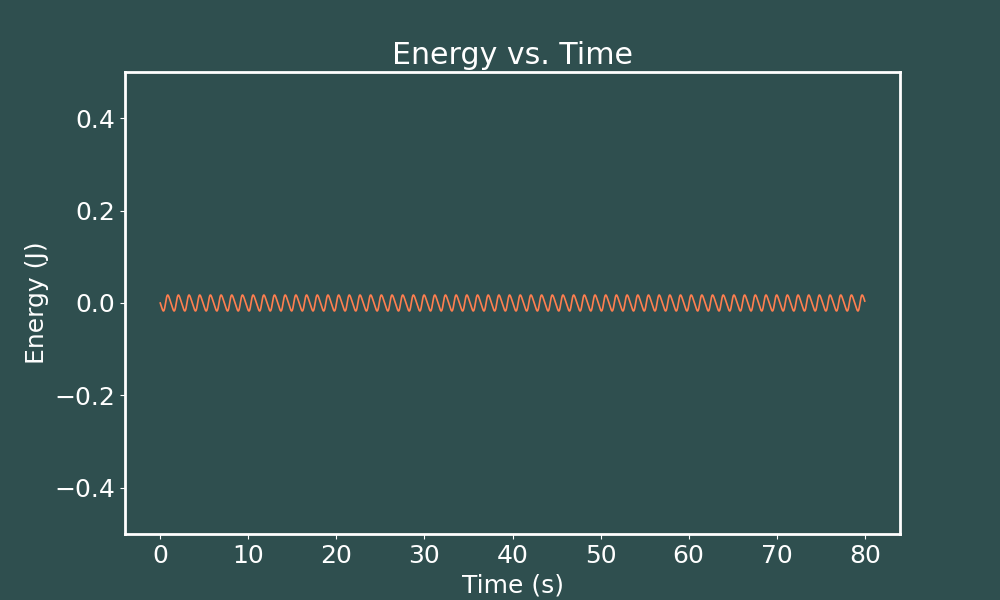
E vs. t Euler-Cromer ($dt = 0.001$)

E vs. t Euler-Cromer ($dt = 0.0005$)

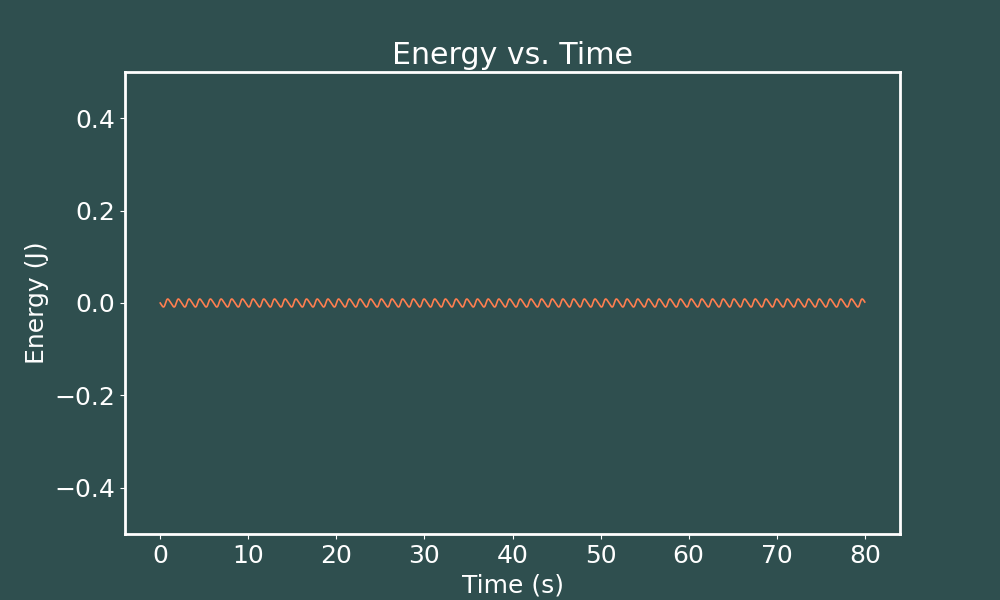
So we see that the smaller our time step is, the less flucuation we have in energies. Cool. Let us now see our energy vs. time graphs when we solve the same system using the 4th order Runge-Kutta method.

E vs. t Runge-Kutta ($dt = 0.01$)

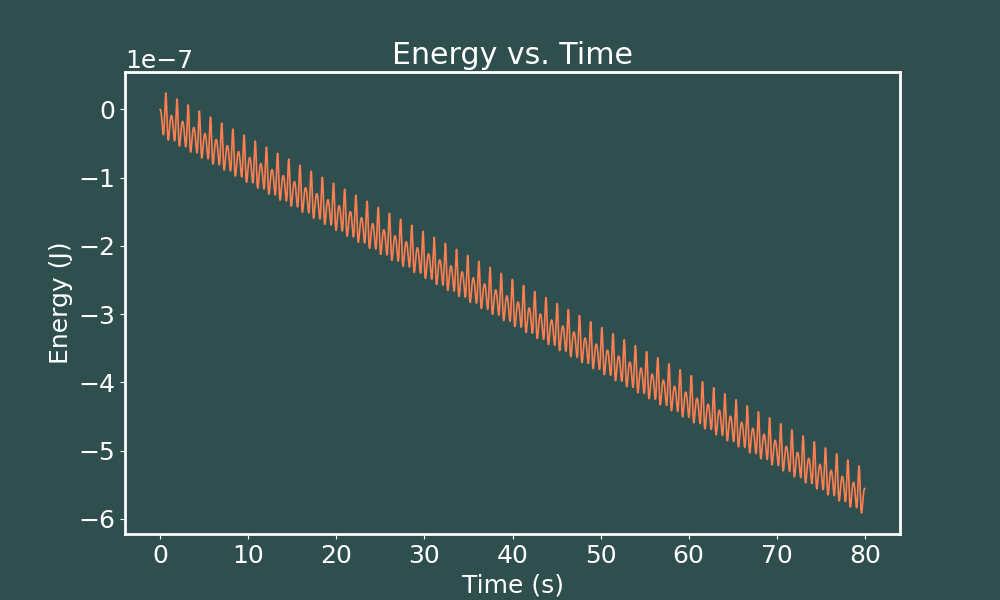
We immediately notice a steady decrease in energy! But also notice that the calculated energies are on the scale of a tenth of a micro-Joule. So even though the energy is decreasing with time, even after 80 seconds of evolution, we are still within a micro-Joule of our starting energy. Let's see how decreasing our time step affects this.

E vs. t Runge-Kutta ($dt = 0.005$)

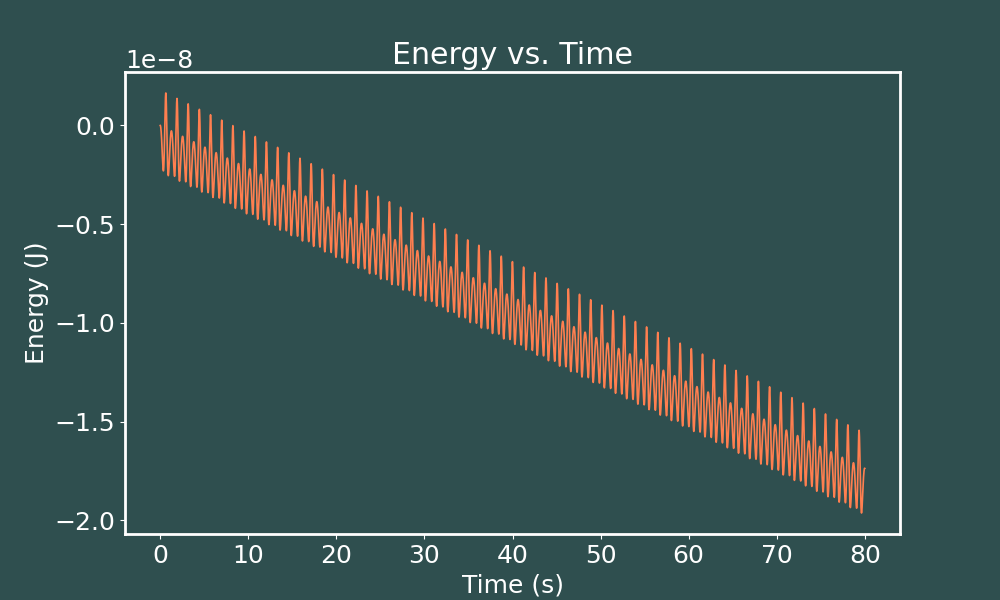
E vs. t Runge-Kutta ($dt = 0.001$)

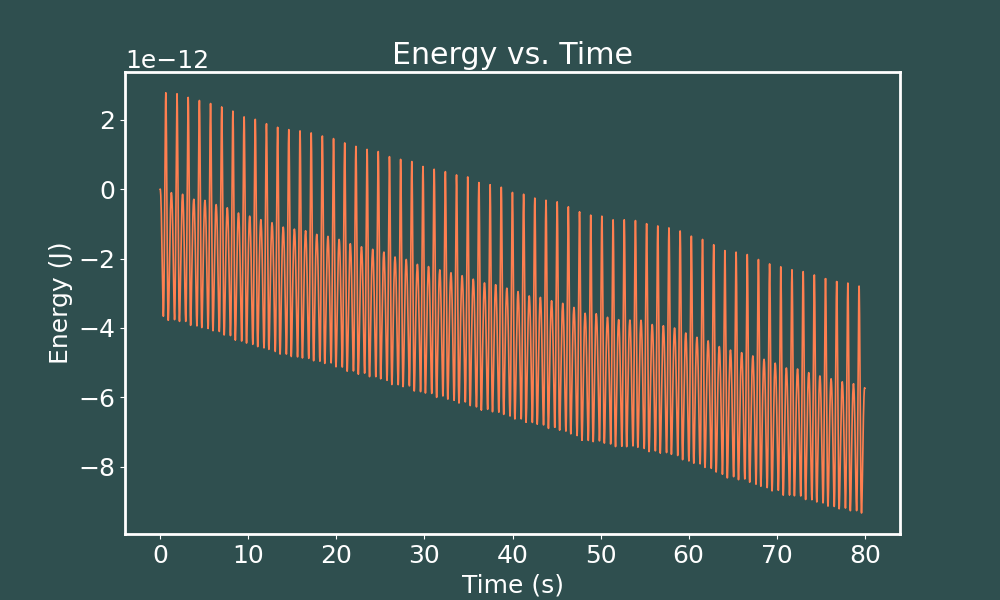
E vs. t Runge-Kutta ($dt = 0.0005$)

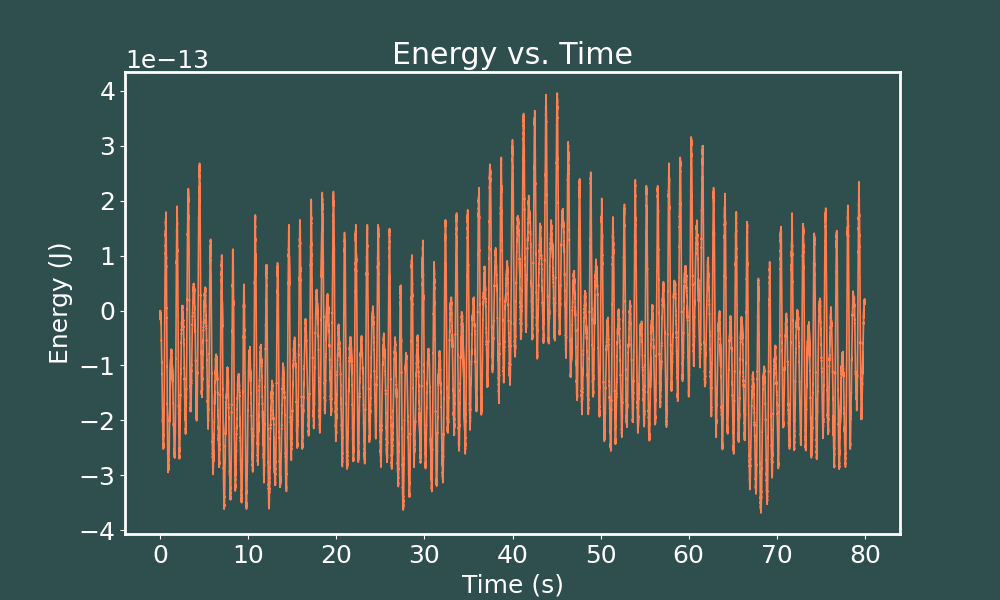
So decreasing the time step for the Runge-Kutta method gives us wildly precise energies here.

∯ Damped Pendulum

The equations of motion for a damped pendulum may be written as $$ \dot{\theta} = \omega $$ $$ \dot{omega} = -\frac{g}{l}\sin\theta - 2\beta\omega $$ where $\beta=b/2m$ where $b$ is a constant that determines the strenth of damping, and $m$ is the mass of the bob at the end of our pendulum. I let $l=1.05$m, $m=1.25$kg, $b=0.05$kg/s. The initial energy of this system is again zero, as we drop it from rest with an initial angular displacement of $\theta_i = \pi/2$ radians. Here is what the time evolution of this system looks like:

I made the animation using the Euler-Cromer method, with a time step of $dt = 0.01$s. Let us take a look at the energy vs time graph:

E vs. t Euler-Cromer ($dt = 0.01$)

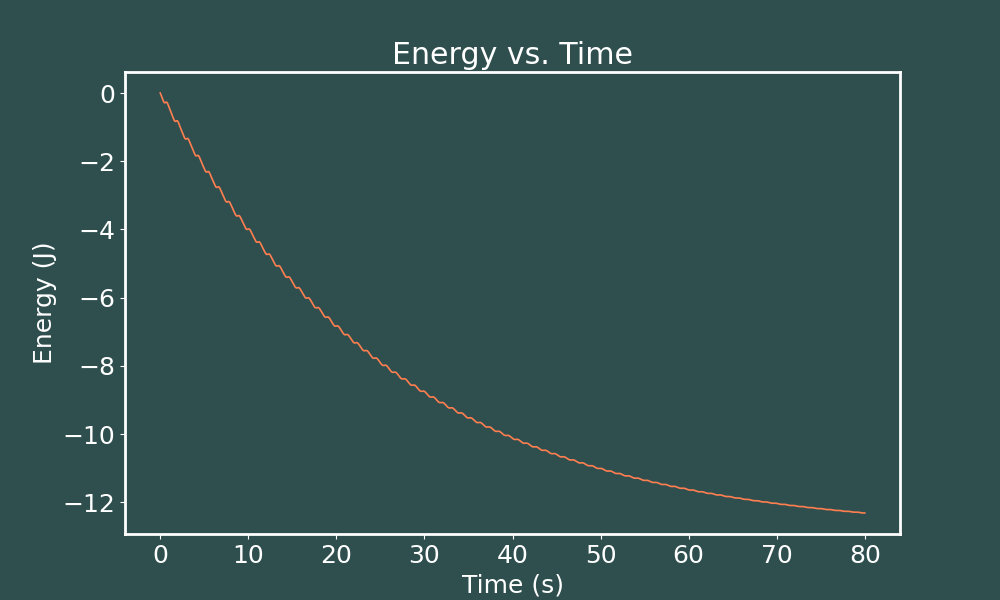
We see that the system is losing energy over time, exactly what one would expect from a damped pendulum. Indeed when the pendulum finally comes to rest we would expect it to have a graviational potential energy of $U=-12.9$J, so that checks out. However, we still see oscillations in the energy here, instead of the smooth curve one might expect. Let's see how decreasing the time step affects this.

E vs. t Euler-Cromer ($dt = 0.005$)

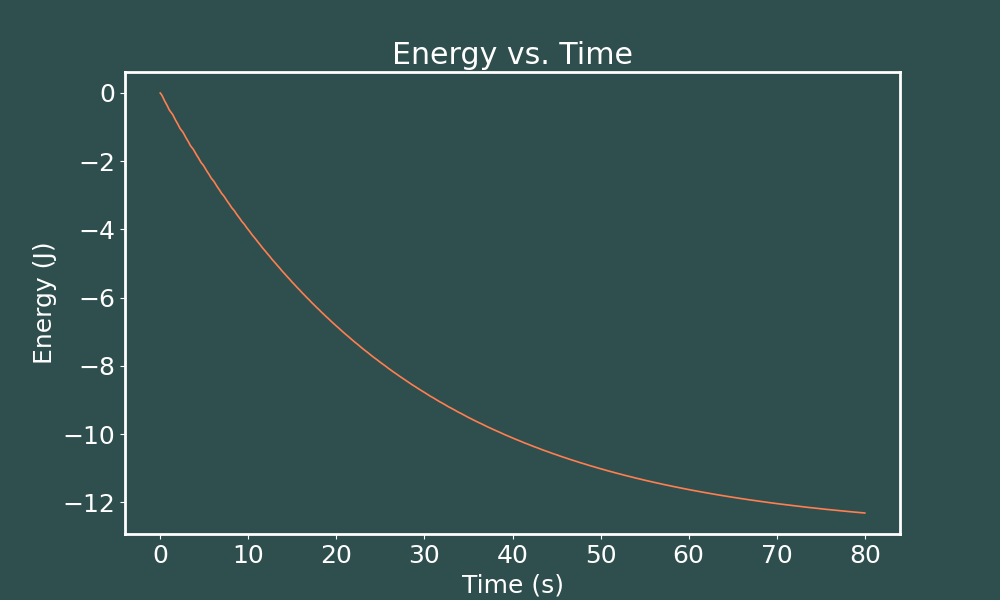
E vs. t Euler-Cromer ($dt = 0.001$)

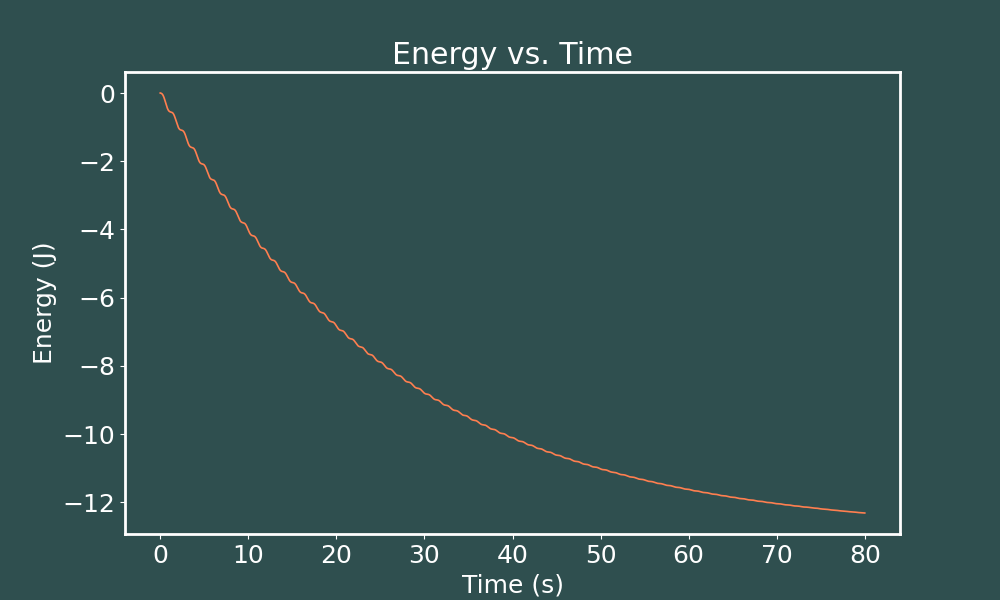
How interesting! A time step of $dt=0.005$s makes the oscillations in energies almost invisible to the eye, but decreasing the time step further than than makes our oscillations re-appear! Now let's solve the same system with 4th order Runge-Kutta to see what we get.

E vs. t Runge-Kutta ($dt = 0.01$)

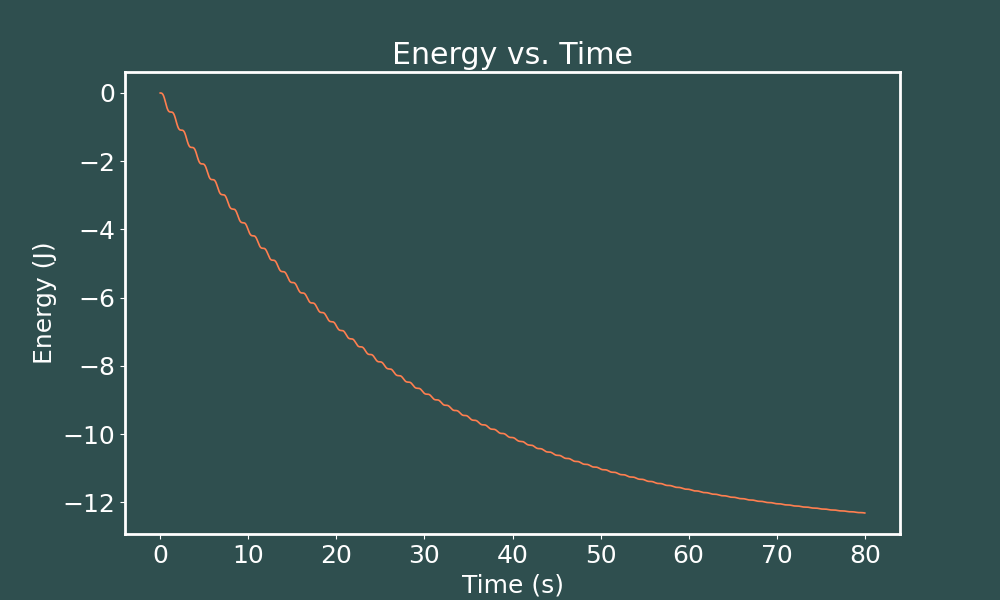
E vs. t Runge-Kutta ($dt = 0.005$)

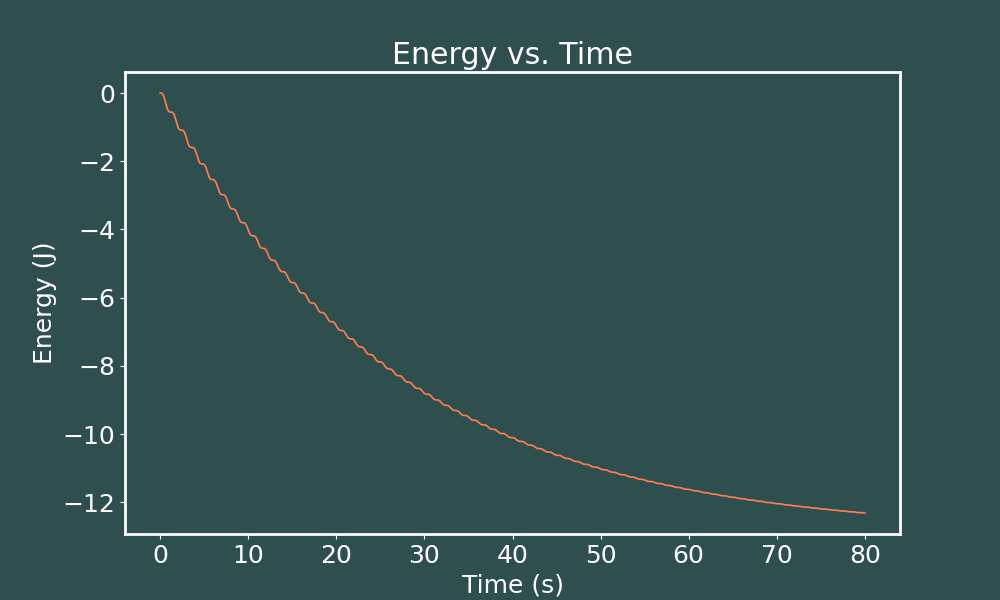
E vs. t Runge-Kutta ($dt = 0.001$)

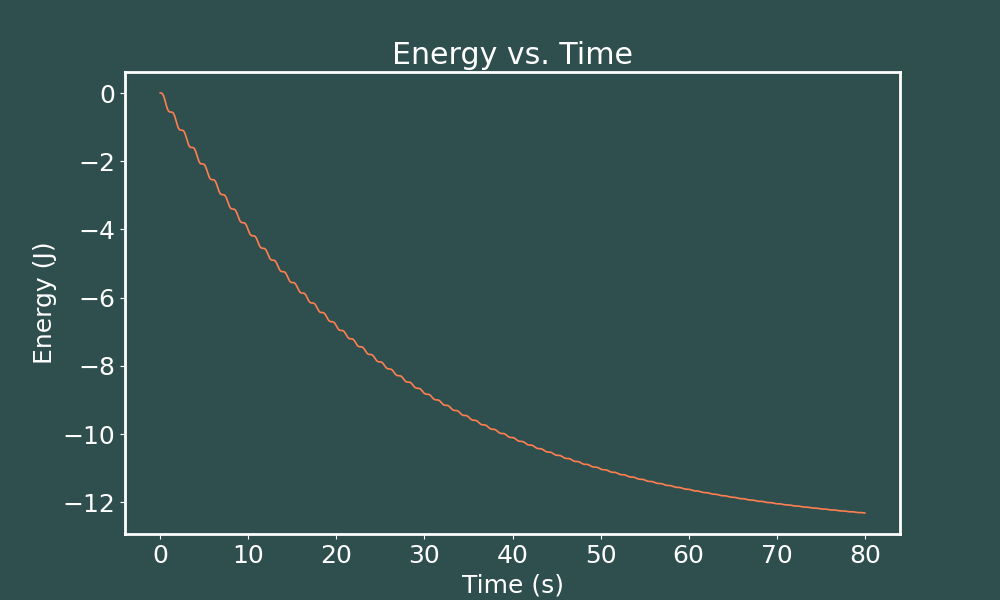
We see that decreasing the time step makes no difference in outcome here. Our oscillations in energy looks the same in each of these trials.

∯ Driven Pendulum

The equations of motion for a driven pendulum (while ignoring friction) might be written as $$ \dot{\theta}= \omega $$ $$ \dot{\omega} = -\frac{g}{l}\sin\theta + C\sin\left(\Omega t + \phi \right) $$ where $C$ is a constant that determines the strength of our driving force, $\Omega$ is another constant that determines the frequency of our driving force, and $\phi$ is the initial phase of our driving force. Here, I use $l=0.15$m, $C=4.0$Hz$^2$, $\Omega = 7.45$Hz, and $\phi = \pi/4$radians. Here is what the time evolution of such a system looks like when released from rest with an initial angular displacement of zero.

I created this animation using the Euler-Cromer method with a time step of $dt=0.01$s. We would expect the energy of this system to oscillate in a fairly sinusoidal fashion, as its amplitude increases and decreases due to the driving force. Lets see what we actually find when we plot our energy vs. time.

E vs. t Euler-Cromer ($dt = 0.01$)

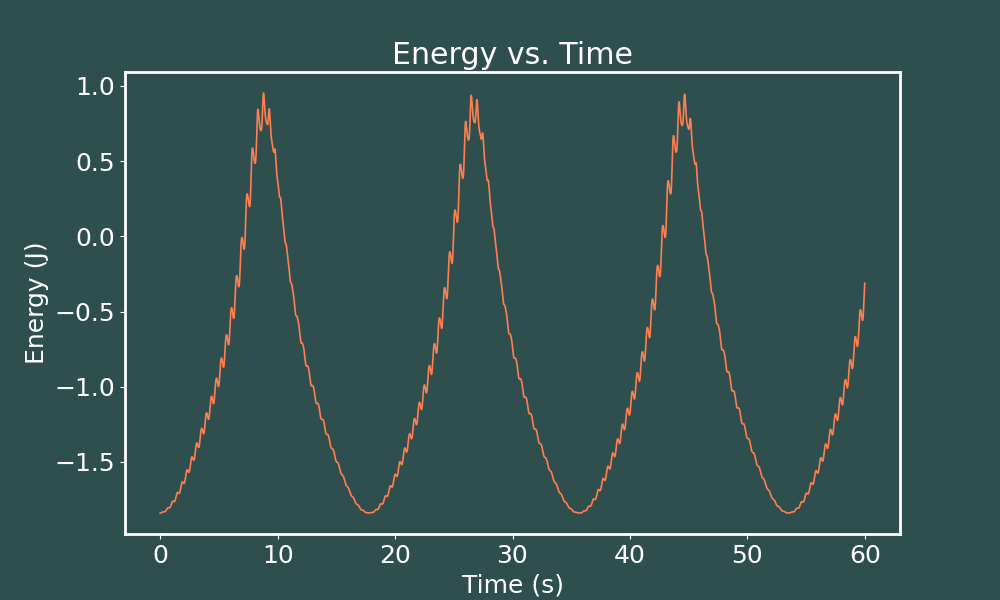
Our initial analysis of how we would expect the energy to behave checks out, we just have these oscillations within our oscillations. Lets see if decreasing our time step might smooth things out a bit.

E vs. t Euler-Cromer ($dt = 0.005$)

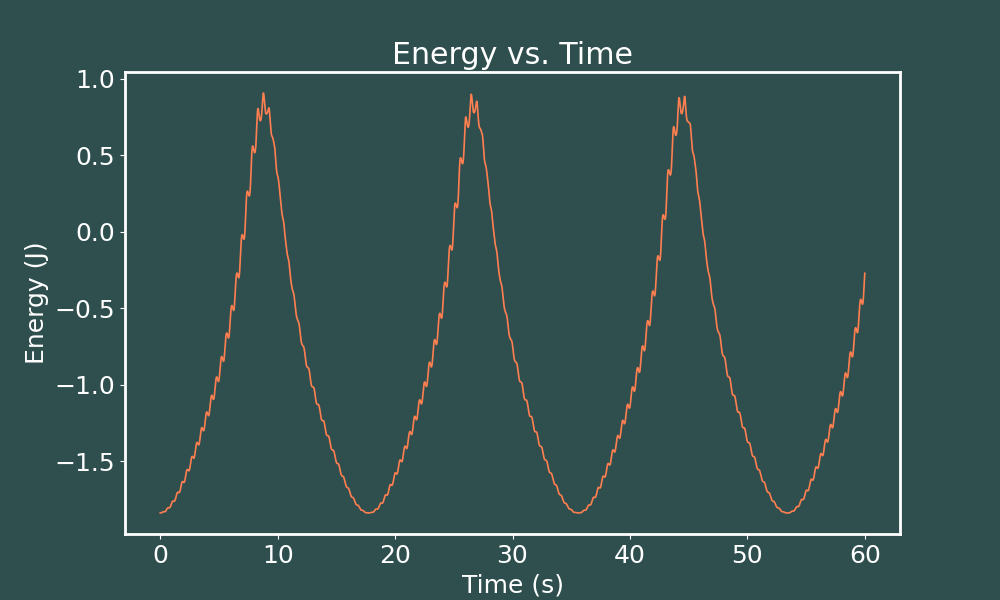
E vs. t Euler-Cromer ($dt = 0.001$)

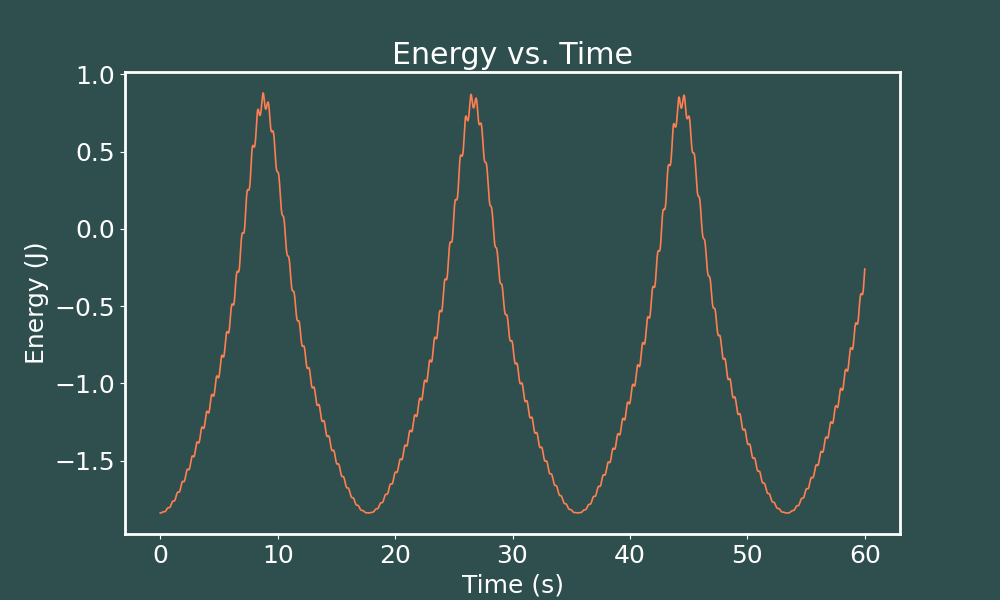
Perhaps it is difficult to tell, but the curves do become mildly smoother as we decrease the time-step, not by much though. Now lets inspect the energy vs. time curves we get when solving this same system with the 4th order Runge-Kutta method.

E vs. t Runge-Kutta ($dt = 0.01$)

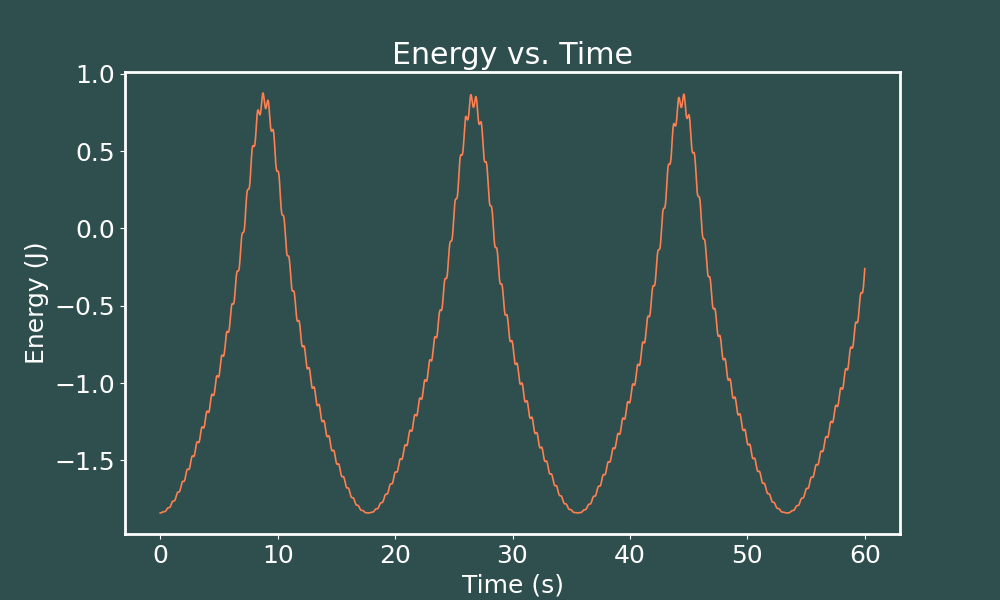
E vs. t Runge-Kutta ($dt = 0.001$)

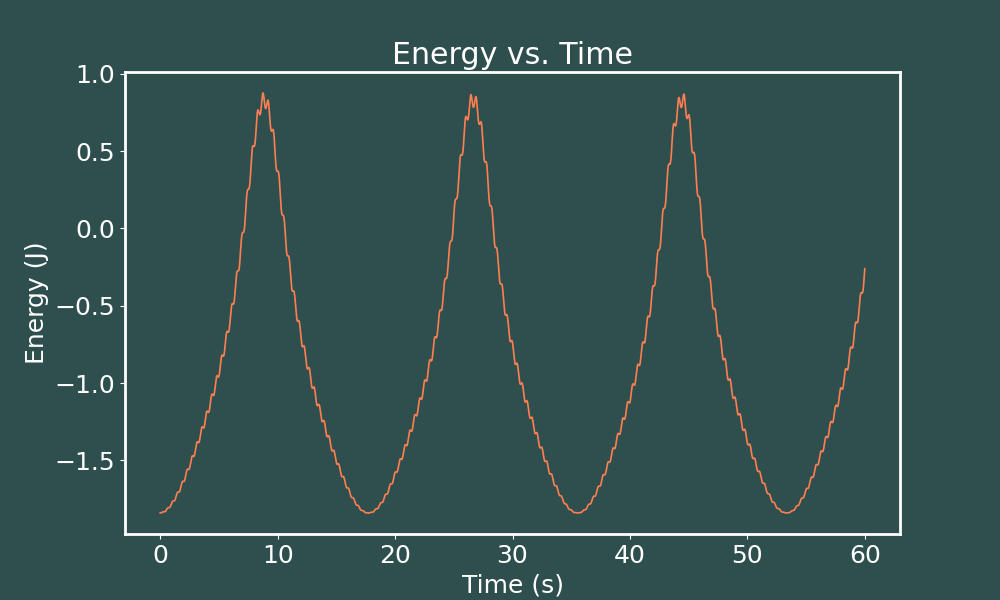
There does not appear to be a difference at all! We found similar results in our analysis of the elastic elastic double pendulum.

Back to the top